Integrated Modeling of Tokamak Plasmas

The MHD activity in this KSTAR experiment allows localizing the midpoint of the H-mode pedestal at approximately 222-223 cm of the major radius. The pedestal structure is not measured in this experiment. The line average density is found to be . Based on this information and typical KSTAR temperature profiles found in the KSTAR experiments, an unique solution for the equilibrium does not exist. Additional assumptions are needed. Stability analysis of equilibrium solutions might help to reduce the uncertainty. Here, I compare two sets of equilibria that are generated by Minwoo and myself. Minwoo used the Corsica code to generate the equilibrium. In order to match the midpoint of the H-mode pedestal with the experimental observations, he shifted the H-
mode pedestal to the region
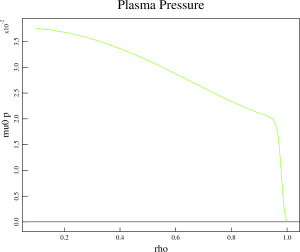
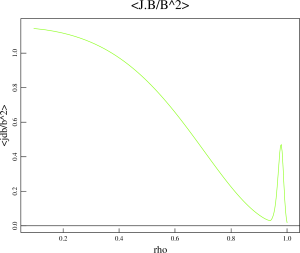
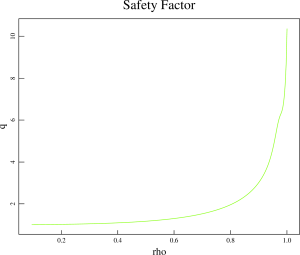
away from the separatrix. The H-mode pedestal is localized in the range from 0.8 to 0.88 of the normalized poloidal flux. In order to maintain the line average density close to the experimental values, the density in the core has been increased. With the typical temperature profiles, the plasma pressure is somewhat peaked in the plasma core. The q value in the midpoint of the H-mode pedestal region is about 3.5. Because of moderate values of q and extended vacuum region between the H-mode pedestal and separatrix, this equilibrium is good for MHD stability analysis and for the extended MHD modeling.
The profiles for the plasma pressure, safety factor and parallel current density are shown below:

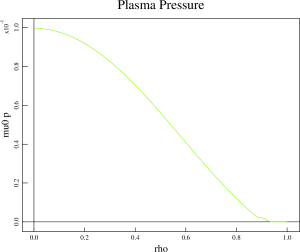
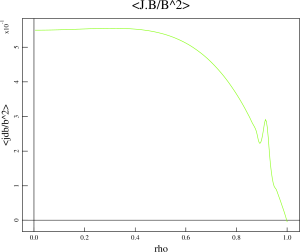
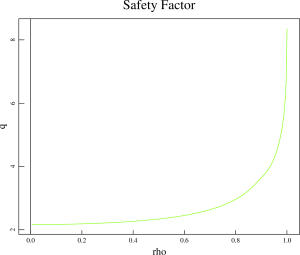
I have generated a second set of equilibria, using assumptions for the H-mode pedestal location that are based on the observations from other tokamaks such as DIII-D. The H-mode pedestal is localized from 0.95 to 1 of the normalized poloidal flux. The physical location of the H-mode pedestal midpoint is the same as in the Minwoo’s equilibria. The TOQ code has been used to generate these equilibria. The pedestal is located very close to the separatrix and the q value is relatively large in the midpoint of the H-mode pedestal (q~6.5). This equilibrium is more difficult to analyze because of large values of q profile. Also, the TOQ is the inverse equilibrium solver and analysis with the extended MHD codes will more difficult because the equilibrium does not include the vacuum region. It will be desirable to import the pressure profiles to the TEQ code in Corsica for coherent comparison of two sets of equilibria.
The profiles for the plasma pressure, safety factor and parallel current density for this equilibrium are shown below: