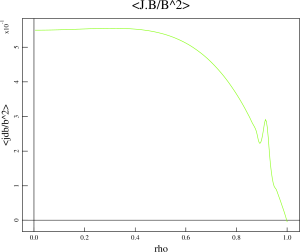
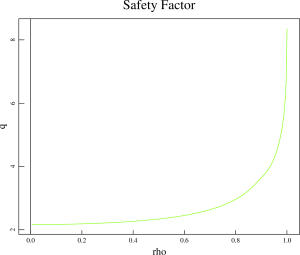
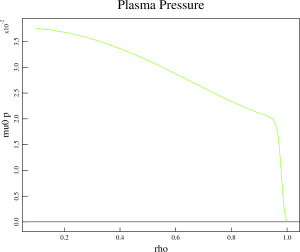
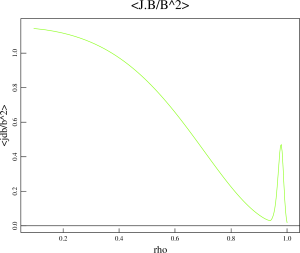
- We start with the original sav-file for this discharge:
caltrans 007328_4400.sav -probname ss-test kstar.bas
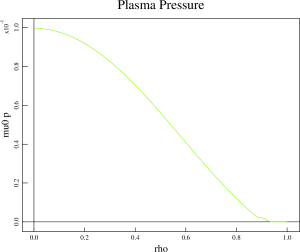
- Then, we update the pressure profile and generate new inverse solution:
thetac=1e-3; epsrk=5.e-9; nht=5000; start_inv
psave( 1: 26)=[4.0652e+05,4.0636e+05,4.0589e+05,4.0510e+05,4.0400e+05,4.0259e+05,4.0085e+05,3.9876e+05,3.9636e+05,3.9354e+05,3.9038e+05,3.8681e+05,3.8290e+05,3.7861e+05,3.7397e+05,3.6897e+05,3.6364e+05,3.5798e+05,3.5201e+05,3.4573e+05,3.3917e+05,3.3235e+05,3.2528e+05,3.1798e+05,3.1047e+05,3.0278e+05]
psave( 27: 52)=[2.9493e+05,2.8693e+05,2.7881e+05,2.7061e+05,2.6233e+05,2.5400e+05,2.4565e+05,2.3729e+05,2.2897e+05,2.2067e+05,2.1246e+05,2.0432e+05,1.9630e+05,1.8841e+05,1.8065e+05,1.7307e+05,1.6566e+05,1.5845e+05,1.5144e+05,1.4466e+05,1.3810e+05,1.3179e+05,1.2572e+05,1.1991e+05,1.1436e+05,1.0907e+05]
psave( 53: 78)=[1.0405e+05,9.9302e+04,9.4818e+04,9.0599e+04,8.6643e+04,8.2945e+04,7.9499e+04,7.6298e+04,7.3334e+04,7.0596e+04,6.8068e+04,6.5736e+04,6.3577e+04,6.1565e+04,5.9667e+04,5.7842e+04,5.6037e+04,5.4183e+04,5.2207e+04,5.0025e+04,4.7558e+04,4.4737e+04,4.1586e+04,3.8103e+04,3.4179e+04,2.9900e+04]
psave( 79:101)=[2.5535e+04,2.1282e+04,1.7332e+04,1.3874e+04,1.0920e+04,8.4769e+03,6.5566e+03,5.0422e+03,3.8616e+03,2.9488e+03,2.2444e+03,1.6993e+03,1.2741e+03,9.5421e+02,7.0459e+02,5.0154e+02,3.5481e+02,2.3120e+02,1.4798e+02,8.3140e+01,3.6807e+01,8.9772e+00,3.4489e+00]
teq_inv(0,1); teq_inv(0,1)
The inverse equilibrium solver is called with the options to keep the plasma current unaltered. We run the solver two times, because the solver has a tendency to inverse the plasma current in the equilibrium solution.
- Then, the direct solution is generated using direct TEQ solver:
inv_eq=0; inv_k=0; run
- The solution is stored in a new sav-file
saveq("s13-t00-01.sav")
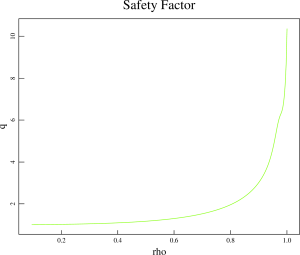
- The q-prifiles are being updated now:
thetac=1e-3; epsrk=5.e-9; nht=5000; start_inv
qsave( 1: 26)=[1.3999e+00,1.4000e+00,1.4006e+00,1.4014e+00,1.4026e+00,1.4041e+00,1.4060e+00,1.4082e+00,1.4108e+00,1.4137e+00,1.4170e+00,1.4207e+00,1.4248e+00,1.4292e+00,1.4341e+00,1.4394e+00,1.4451e+00,1.4513e+00,1.4579e+00,1.4650e+00,1.4726e+00,1.4806e+00,1.4892e+00,1.4983e+00,1.5079e+00,1.5181e+00]
qsave( 27: 52)=[1.5289e+00,1.5403e+00,1.5524e+00,1.5650e+00,1.5784e+00,1.5924e+00,1.6072e+00,1.6227e+00,1.6390e+00,1.6560e+00,1.6740e+00,1.6927e+00,1.7124e+00,1.7331e+00,1.7546e+00,1.7773e+00,1.8009e+00,1.8257e+00,1.8515e+00,1.8786e+00,1.9070e+00,1.9366e+00,1.9675e+00,1.9998e+00,2.0336e+00,2.0689e+00]
qsave( 53: 78)=[2.1059e+00,2.1445e+00,2.1848e+00,2.2270e+00,2.2711e+00,2.3171e+00,2.3653e+00,2.4157e+00,2.4684e+00,2.5236e+00,2.5813e+00,2.6418e+00,2.7051e+00,2.7715e+00,2.8411e+00,2.9142e+00,2.9910e+00,3.0719e+00,3.1572e+00,3.2472e+00,3.3424e+00,3.4432e+00,3.5509e+00,3.6655e+00,3.7876e+00,3.9196e+00]
qsave( 79:101)=[4.0602e+00,4.2122e+00,4.3736e+00,4.5492e+00,4.7362e+00,4.9360e+00,5.1541e+00,5.3890e+00,5.6429e+00,5.9183e+00,6.2180e+00,6.5436e+00,6.8934e+00,7.2872e+00,7.7253e+00,8.1641e+00,8.6979e+00,9.1615e+00,9.8188e+00,1.0331e+01,1.0697e+01,1.0917e+01,1.0960e+01]
teq_inv(0,1); teq_inv(0,1)
- New direct solution is generated again. The solution will include the update plasma pressure and q profiles:
inv_eq=0; inv_k=0; run
saveq("s13-t00-02.sav")
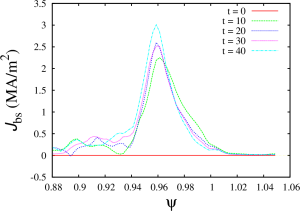
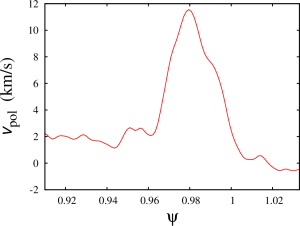
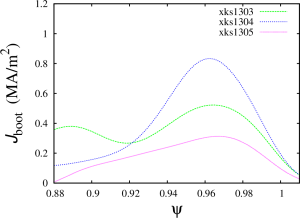
- Now, we need to ensure that the bootstrap current is properly included. In order to do this, we will exclude the edge current from the jparsrf and will replace it with the bootstrap current from the Sauter model:
jparsave(81:101)=jparsave(80)
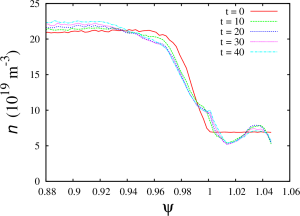
real ndens=psibar; ndens=2.6e19
real prbs=psave/10./2.
real tebs=prbs/ndens/1.602e-19
real zeffbs=psave; zeffbs=1.
real pbeambs=psibar; pbeambs=0.
read jbootstrap.bas
real jbs1 = jbootstrap(prbs,ndens,tebs,tebs,zeffbs, pbeambs, 1., 1., 0.)
real jbs0 = jbs1(:,1)
real foo1=tanh((1.01-psibar)/0.05)
real foo2=(1+tanh((psibar-0.7)/0.05))/2.
jparsave=jparsave*foo1+jbs0/bsqrf*foo2
- Run a sequence of inverse and direct equilibrium solvers ensuring the the plasma current does not change:
thetac=1e-3; residj=1e-9; nht=5000; start_inv
jparsave=jparsave*foo1+jbs0/bsqrf*foo2
nf; plot [jparsrf,jparsave], asrf+rsrf
teq_inv(3,0); teq_inv(0,1); teq_inv(0,1)
inv_eq=0; inv_k=0; run
saveq("s13-t00-03.sav")
- Increase the resolution in the direct equilibrium solution to 257×257 (at least):
gridup; run; saveq("s13-t00-04.sav")
gridup; run; saveq("s13-t00-05.sav")
- Save the new geqdsk file
weqdsk
- Note, the the resolution for the inverse solver is also important and it might be useful to increase it by changing the values of map and msrf (theta and psi dimensions in the inverse solve) and running the inverse solver.